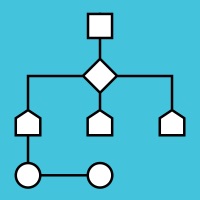
Сетевой график – это динамическая модель проекта, которая отражает последовательность и зависимость работ, необходимых для успешного завершения проекта. Сетевой график отражает сроки выполнения запланированных работ и ресурсы, необходимые для их выполнения, а также прямые финансовые затраты, возникающие при реализации этих работ.
В английском языке для определения сетевого графика используется термин Project Network — is a graph depicting the sequence in which a project’s terminal elements are to be completed by showing terminal elements and their dependencies.
Основной целью использования сетевого графика является эффективное планирование и управление работами и ресурсами проекта. При этом, под ресурсами в данном контексте понимается как оборудование, производственные мощности или денежные средства, так и трудовые ресурсы, внутренние или внешние для организации, выполняющей проект.
Наибольшая эффективность применения сетевого графика достигается при его использовании для планирования проектов или отдельных взаимосвязанных работ. Сетевой график позволяет довольно точно определить плановые сроки завершения проекта и выявить возможные варианты их сокращения. И, что более важно, сетевой график позволяет на ранней стадии планирования проекта выявить критический путь. Кроме этого сетевой график позволяет осуществлять базовый контроль над ходом работ проекта, их сроками и исполнением бюджета.
Виды сетевых графиков
Сетевой график — это граф, на котором события (состояния работ или объектов в определенный момент времени) представлены в виде вершин, а работы проекта представлены в виде дуг, соединяющих вершины графа. Сетевой график, представленный в таком виде, изначально является частью метода PERT (Program Evaluation and Review Technique).
На практике же чаще используется другой вариант сетевого графика, когда вершинами графа являются работы, а дуги обозначают взаимосвязь между ними. Такой вид сетевого графика является частью метода критического пути (англ., CPM — Critical Path Method).
Рассмотрим второй вариант графика и алгоритм его построения подробнее.
Алгоритм построения сетевого графика
Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.
Шаг 1. Определить основную цель проекта
Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.
Шаг 2. Выявить ограничения
Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.
Шаг 3. Определить состав работ
Определить состав работ, необходимых для достижения цели, поставленной на шаге 1.
Шаг 4. Оценить длительность работ
Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.
Шаг 5. Определить последовательность работ
Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.
Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.
Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.
Шаг 6. Указать связи между работами
Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.
Шаг 7. Определить раннее начало и раннее окончание
Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.
Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.
Шаг 8. Определить поздние начало и окончание
Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.
Шаг 9. Определить временной резерв
Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.
Шаг 10. Выявить критический путь
Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.
Пример построения сетевого графика
Несмотря на то, что описанный выше алгоритм может показаться сложным, на самом же деле построение сетевого графика задача несложная. Для того, чтобы убедиться в этом рассмотрим построение сетевого графика на простом примере ремонта детской комнаты.
Шаг 1. Определить основную цель проекта
Представьте, что сейчас лето, вашему сыну исполнилось 7 лет и в сентябре он идет в школу. Вы решил обновить его комнату к новому учебному году и сделать ее подходящей для школьника, т.е. должно появиться полноценной рабочее место, зонирование комнаты измениться, и т.д.
В этом случае целью нашего небольшого проекта будет — сделать комнату пригодной и приятной для проживания мальчика, который пойдет в начальную школу.
Шаг 2. Выявить ограничения
Бюджет не более 100,000 руб., ремонтные работы можно вести только в рабочие дни с 10:00 до 18:00 с обязательным перерывом с 12:00 до 14:00. Итого получается — 6 рабочих часов в день.
Шаг 3. Определить состав работ
Немного поразмыслив мы накидали основные работы, которые надо сделать, а именно:
- Нам нужен дизайн-проект новой комнаты;
- Нам надо закупить материалы для ремонта;
- Надо составить смету ремонта;
- Надо выполнить сам ремонт;
- И т.к. мы решили сделать небольшую перепланировку, то надо согласовать ее с ТСЖ.
Отобразим эти работы в виде блоков:
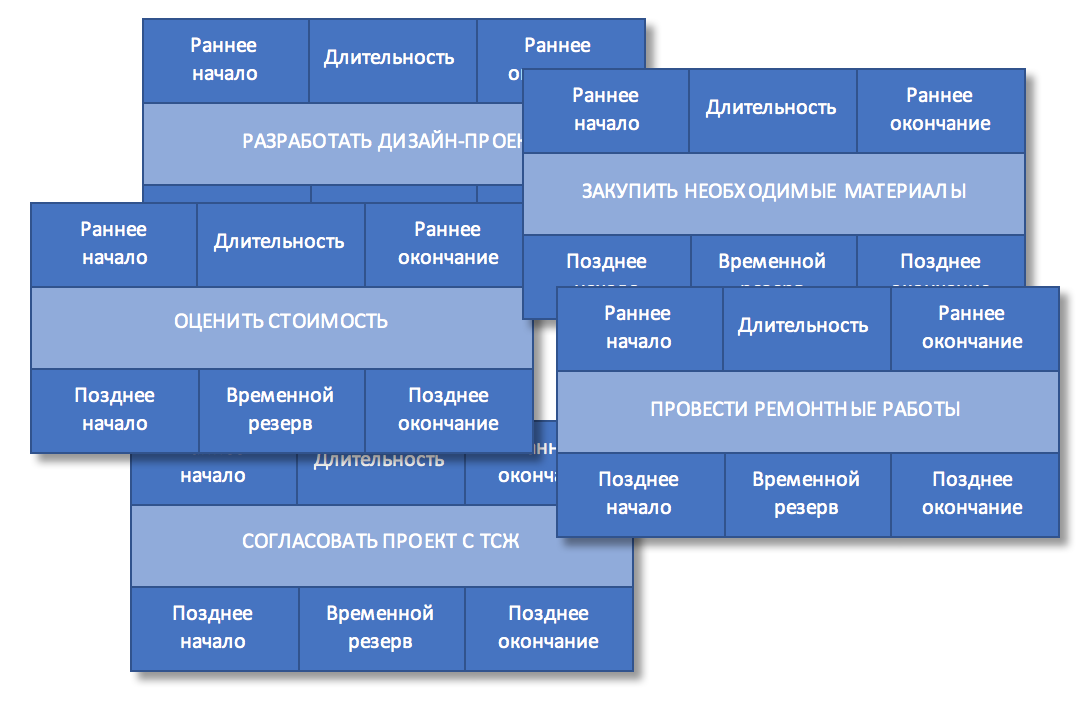
Рисунок 1. Состав работ
Шаг 4. Оценить длительность работ
Мы решили оценивать длительность работ в днях, т.к. до начала учебного года еще достаточно времени, то такая точность планирования нас вполне устраивает.

Рисунок 2. Длительность работ
Шаг 5. Определить последовательность работ
Теперь определим последовательность работ, мы будем использовать схему построения сетевого графика «сверху-вниз». Первая работа, которую необходимо выполнить — это работа «Разработать дизайн-проекта«. Затем мы оценим стоимость проекта, а параллельно начнем согласование с ТСЖ, т.к. эта задача занимает много времени. После того, как мы оценим проект и его согласуем, мы приступим к покупке всех необходимых материалов и уже затем начнем сам ремонт.

Рисунок 3. Последовательность работ
Шаг 6. Указать связи между работами
Укажем стрелками связи между работами.
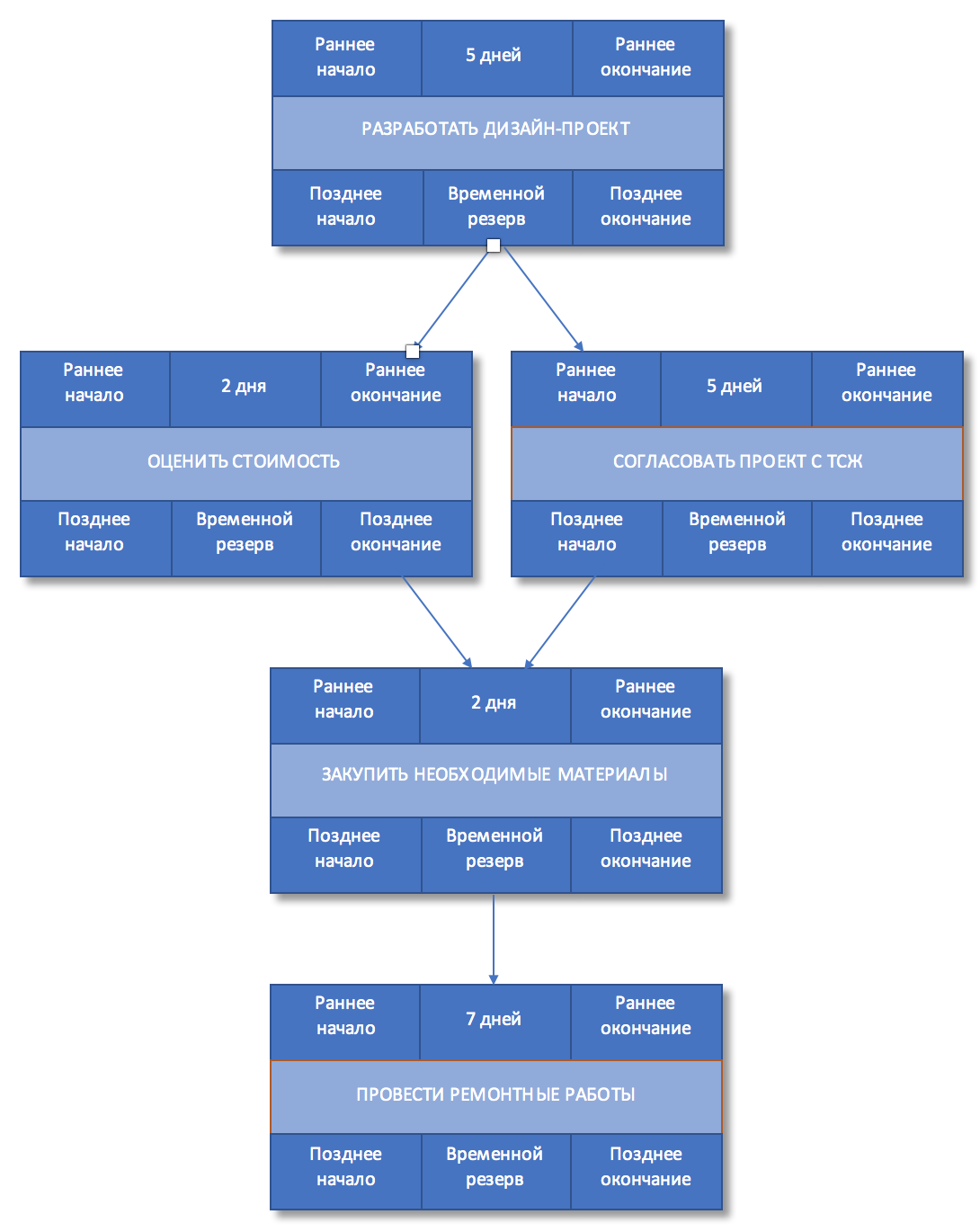
Рисунок 4. Связи между работами
Шаг 7. Определить раннее начало и раннее окончание
Т.к. мы выбрали модель сетевого график «сверху-вниз», то начинаем его и просматривать сверху вниз, начиная с самой верхней работы, и далее по очереди двигаемся к самой нижней работе.
Напомним, что раннее начало последующей работы будет совпадать с ранним завершением предшествующей, а раннее окончание каждой из работ определяется как раннее начало плюс длительность работ Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ.
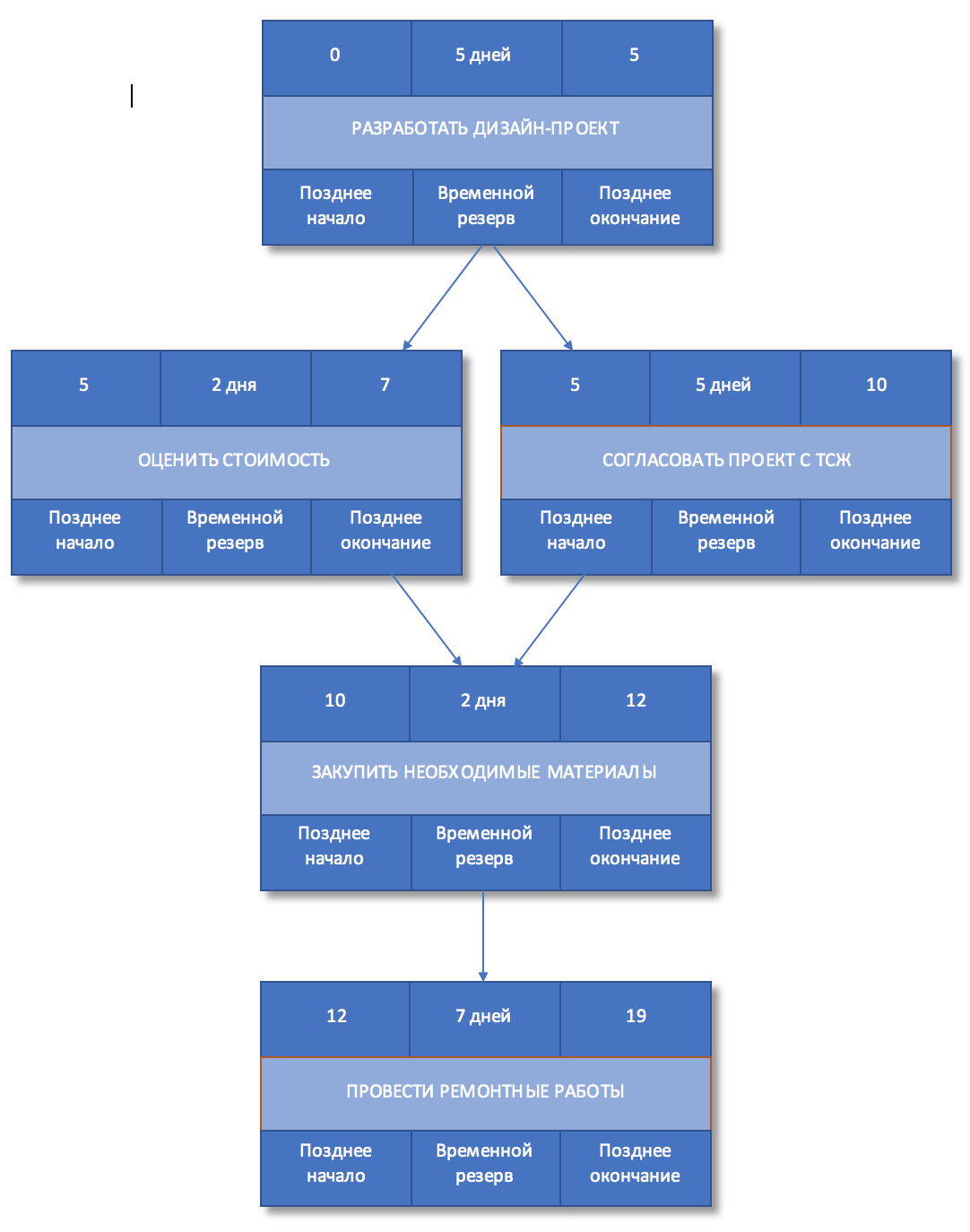
Рисунок 5. Раннее начало и окончание работ
Шаг 8. Определить поздние начало и окончание
Для того, чтобы определить поздние начало и окончание просмотрим сетевой график в обратном направлении — снизу вверх. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.
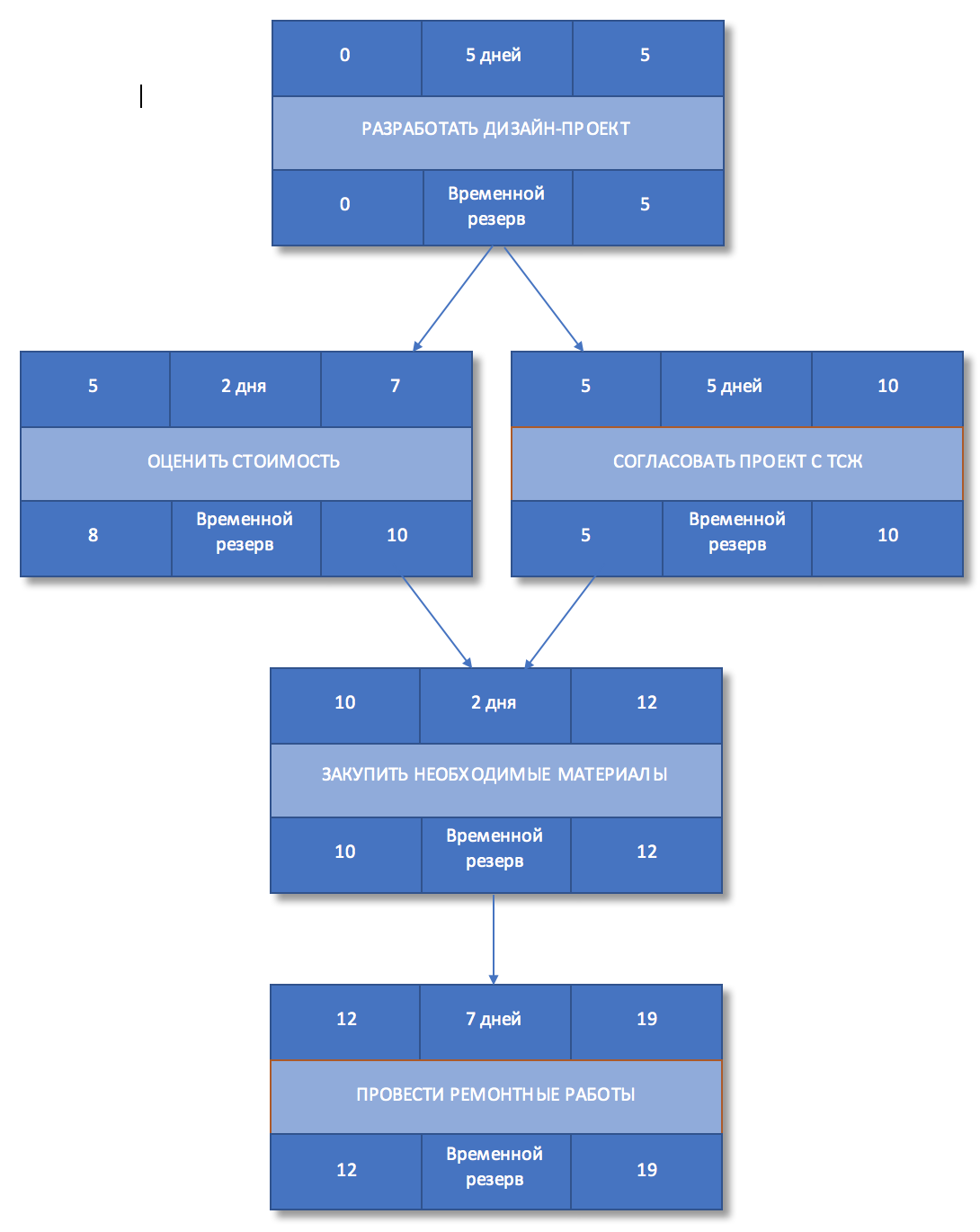
Рисунок 6. Позднее начало и окончание работ
Шаг 9. Определить временной резерв
Вычислим временной резерв для каждой из работ. Он вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.
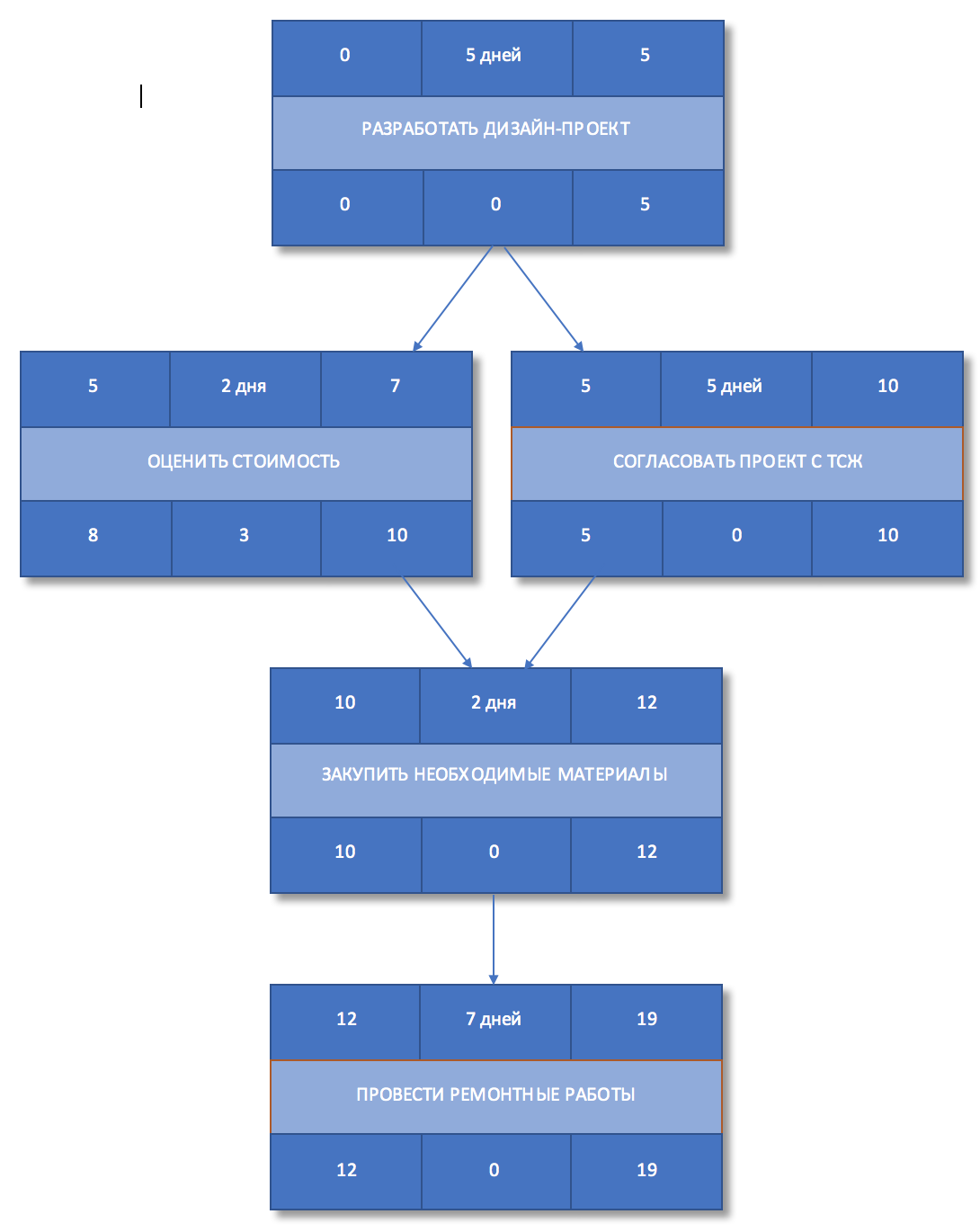
Рисунок 7. Временной резерв
Шаг 10. Выявить критический путь
Как мы уже знаем, критический путь — это цепочка работ, у которых резерв времени равен нулю. Выделим такие задачи на сетевом графике.
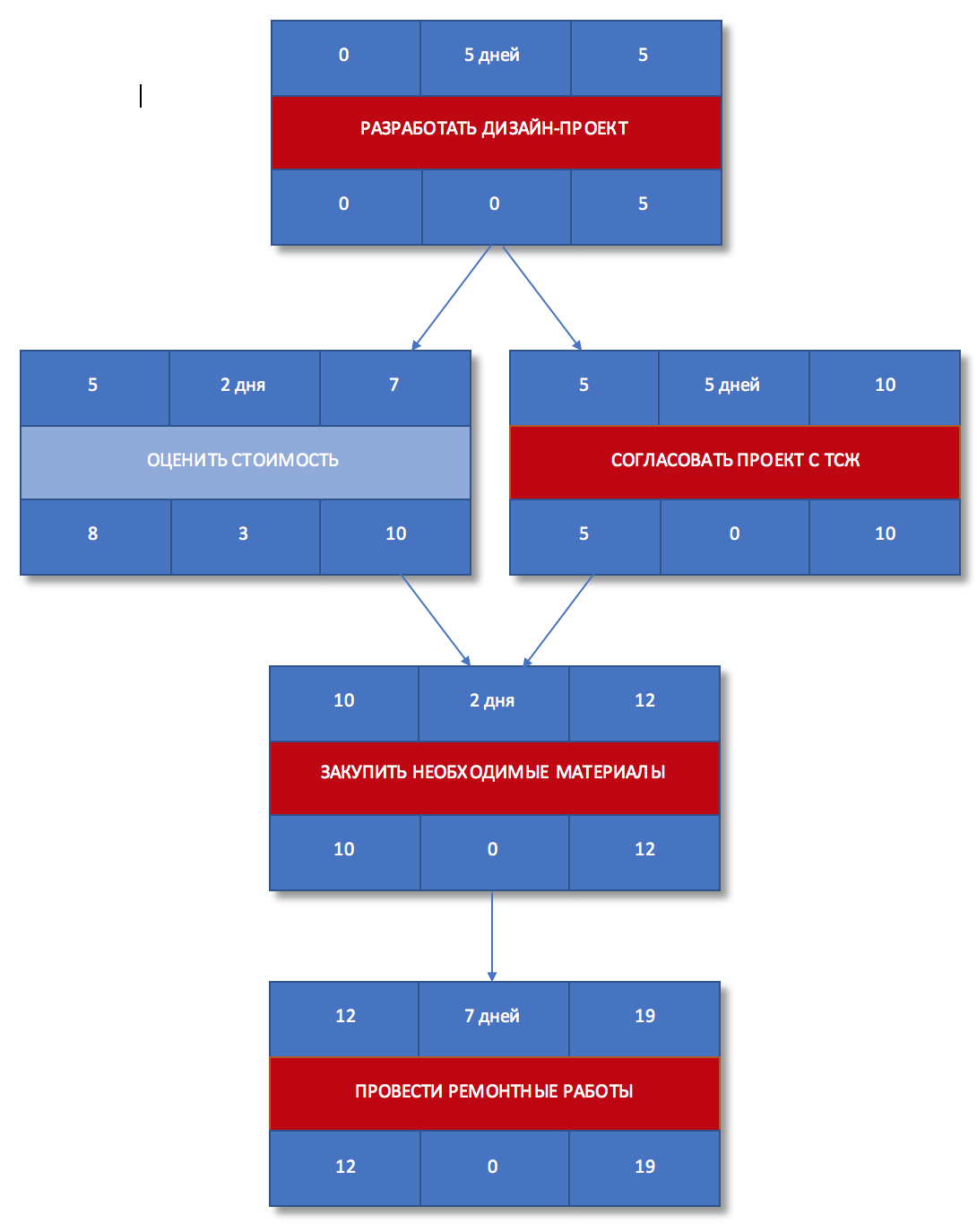
Рисунок 8. Критический путь
Задачи «Разработать дизайн-проект«, «Согласовать проект с ТСЖ» и «Закупить необходимые материалы«, «Провести ремонтные работы» составляю критический путь, а его длина составляет 19 дней. Это означает, что в текущем виде проект не может быть выполнен быстрее, чем за 19 дней. Если мы хотим сократить сроки проекта, то нам необходимо оптимизировать задачи, лежащие на критическом пути.
Например, мы можем начать ремонтные работы раньше получения согласования на перепланировку от ТСЖ, приняв на себя риски того, что согласование может быть не получено.
