Каждый менеджер проекта сталкивается с такой типовой для него задачей, как построение сетевого графика. В настоящее время этот процесс полностью автоматизирован и, как правило, у менеджера не возникает больших проблем. Уже давно нет необходимости чертить на бумаге графики, высчитывать ранние и поздние начала или окончания задач, соединять задачи стрелками, вычислять длину критического пути. ИСУП успешно решает все эти задачи.
Однако, без понимания основ и правил построения сетевых графиков менеджеры проектов довольно-таки часто совершают ошибки. Несмотря на то, что современные ИСУП достаточно «умные» и подстраховывают менеджера проекта во многих моментах, связанных с расписанием проекта, тем не менее, остаются «слепые» зоны, которые лежат только в зоне ответственности менеджера проекта.
Для того, чтобы получить настоящую пользу от ИСУП, ей надо уметь грамотно пользоваться, как и любым другим инструментом.
Что такое сетевой график
Сетевой график (англ., Project Network) — это динамическая модель проекта, отражающая зависимость и последовательность выполнения работ проекта, связывающая их завершение во времени с учётом затрат ресурсов и стоимости работ.
Сетевой график может быть построен в двумя способами:
- Вершины графа отображают состояния некоторого объекта (например, строительства), а дуги — работы, ведущиеся на этом объекте.
- Вершины графа отражают работы, а связи между ними — зависимости между работами.
Правила построения сетевого граифка
Прежде всего, построение сетевого графика заключается в правильном соединении между собой событий (на схеме обозначаются кружками) с помощью работ (на схеме обозначаются стрелками). Правильность соединения стрелок заключается в следующем:
- каждая работа в сетевом графике должна выходить из события, которое означает окончание всех работ, результат которых необходим для начала работы;
- событие, обозначающее начало определенной работы не должно включать в себя результаты работ, завершение которых не требуется для начала этой работы;
- сетевой график строится слева направо, и каждое событие с большим порядковым номером должно быть расположено правее предыдущего. Стрелки, изображающие работы, должны также располагаться слева направо.
Исходные работы
Построение графика начинается с изображения работ, не требующих для своего начала результатов выполнения других работ. Такие работы можно назвать исходными, так как все остальные работы комплекса будут выполняться только после их полного выполнения.
В зависимости от специфики планируемого комплекса, исходных работ может быть несколько, а может быть только одна. Размещая исходные работы необходимо учитывать, что на сетевом графике, должно быть только одно исходное событие.
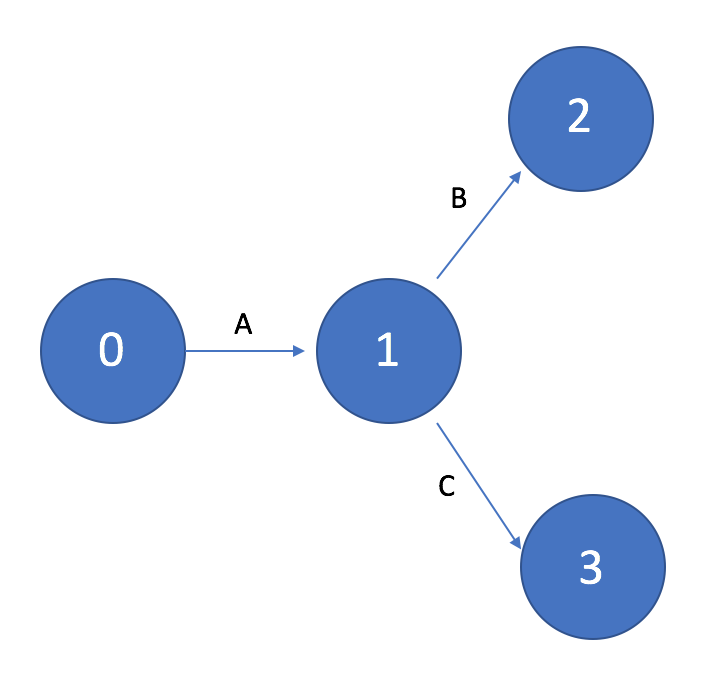
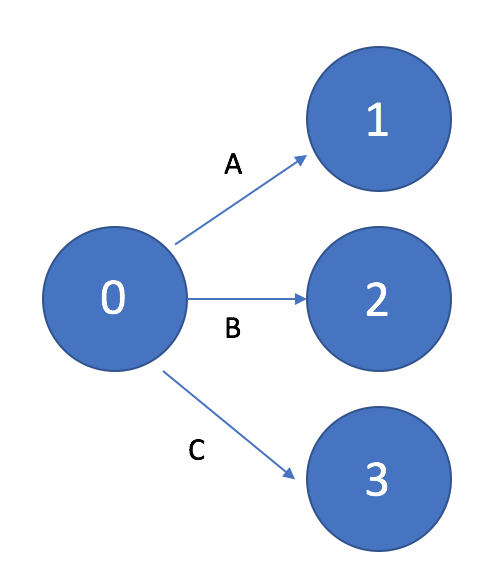
На рисунке 1 показан пример начала сетевого графика с одной исходной работой (работа A), а на рисунке 2 пример начала сетевого графика с тремя исходными работами (работы A, B, C).
Последовательные работы
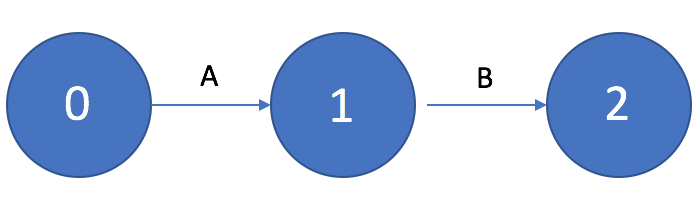
Если работа B должна выполняться только после выполнения работы A, то на графике это изображается в виде последовательной цепочки работ и событий.
Работы, выполняемые после одной и той же работы
Если для выполнения нескольких работ, например, B и C необходим результат одной и той же работы A, то на графике это изображается «параллельными» стрелками, выходящими из события, являющегося результатом выполнения работы А.
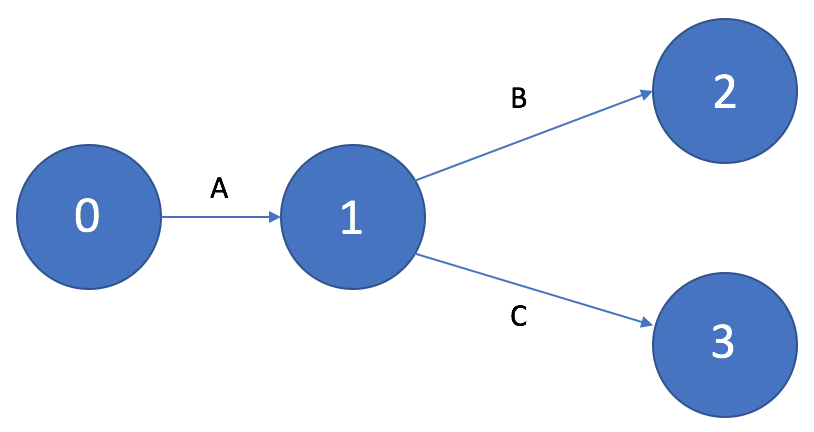
Работа, выполняемая после нескольких работ
Если для выполнения работы C необходим результат работ A и B, то на графике это изображается «параллельными» стрелками, входящими в событие, после достижения которого следует работа C.
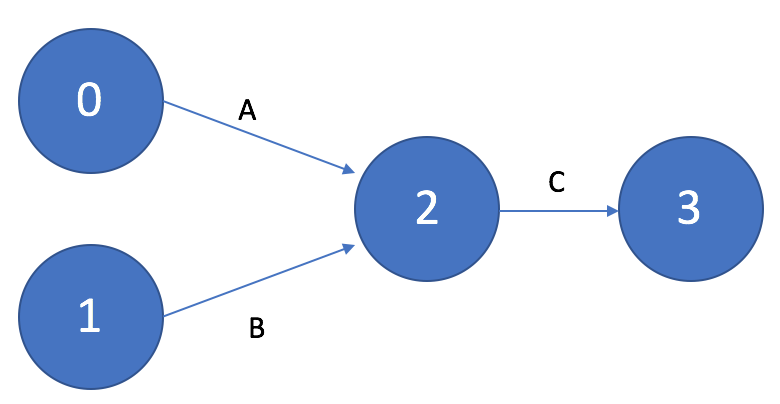
Работы, выполняемые после частичного выполнения других работ
Если для выполнения работ B и C необходим промежуточный результат работы A, то работа A разбивается на подзадачи таким образом, чтобы первая ее подзадача (A1) выполнялась до получения промежуточного результата, необходимого для начала работы B, а вторая подзадача выполнялась до получения промежуточного результата, необходимого для начала работы C, последующая же часть A3, может выполняться параллельно с работами A1 и A2.
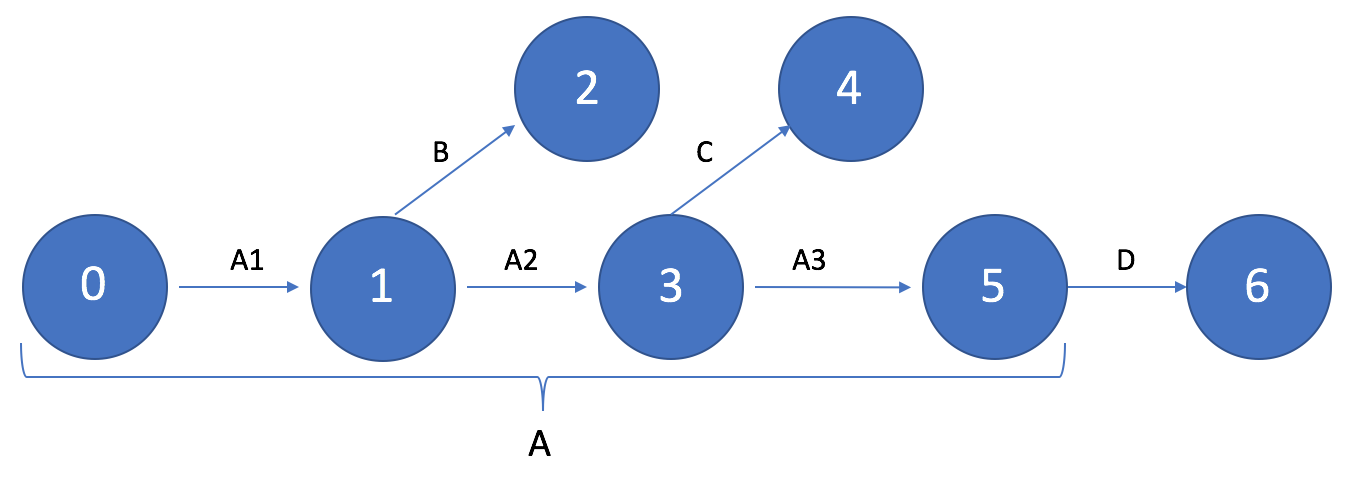
Работы, имеющие общие начальное и конечное события
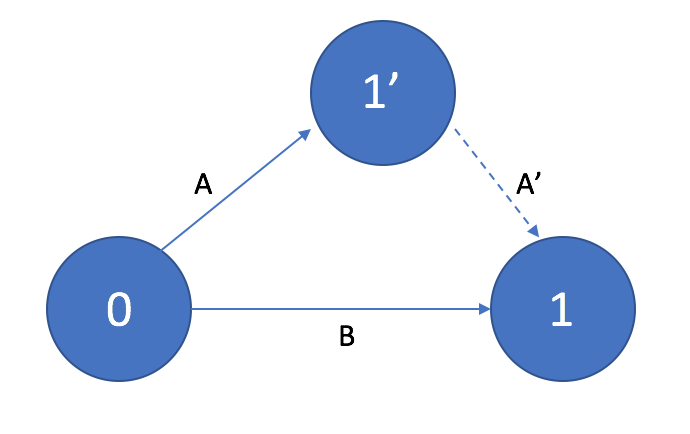
Два соседних события могут быть объединены одной и только одной работой. Для изображения параллельных работ на сетевом графике вводится так называемое промежуточное событие и фиктивная работа.
Использование фиктивных работ
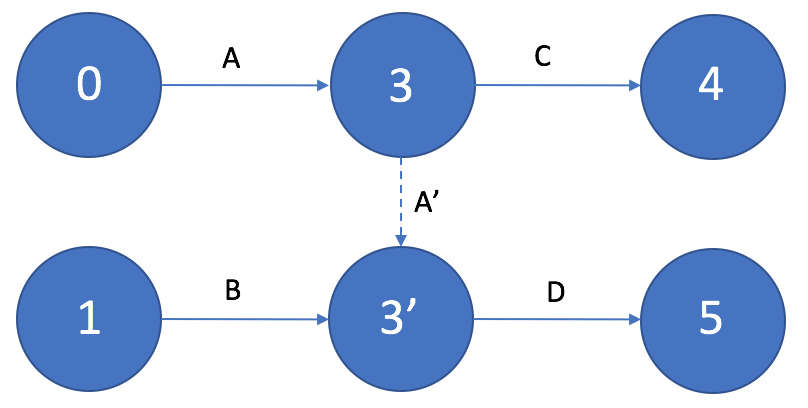
Если выполнение работы D возможно только после получения совокупного результата работ A и B, а выполнение работы C – после получения только результата работы А, то в сетевом графике необходимо ввести дополнительное событие и фиктивную работу.
«Хвосты» и «тупики»
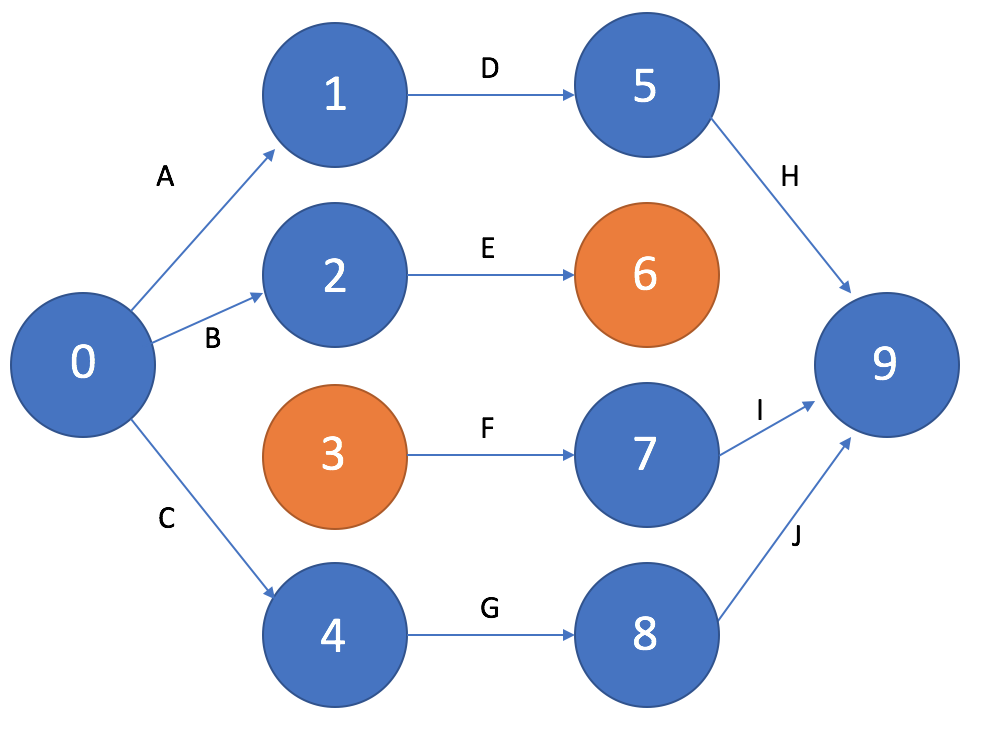
В сети не должно быть «тупиков», т.е. промежуточных событий, из которых не выходит ни одна работа. На рисунке 9 тупиковым событием является событие 6.
Также не должно быть «хвостов», т.е. промежуточных событий, которым не предшествует хотя бы одна работа. На рисунке 9 хвостовым событием является событие 3.
Циклы
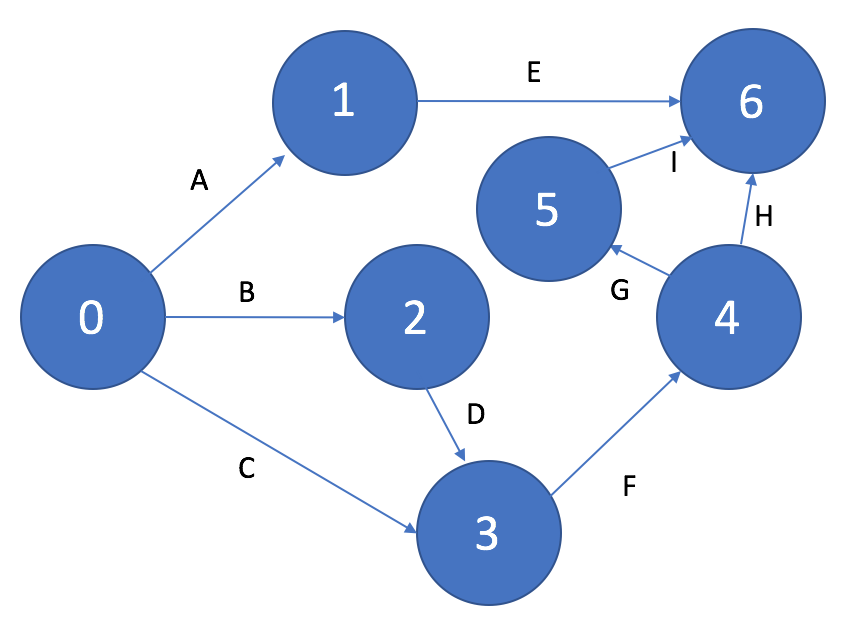
На сетевом графике не должно быть циклов, состоящих из взаимосвязанных работ, создающих замкнутую цепь — цепочка работ D->F->G на рисунке 10. Данная ситуация скорее всего свидетельствует об ошибке при составлении перечня работ и определении их взаимосвязей.
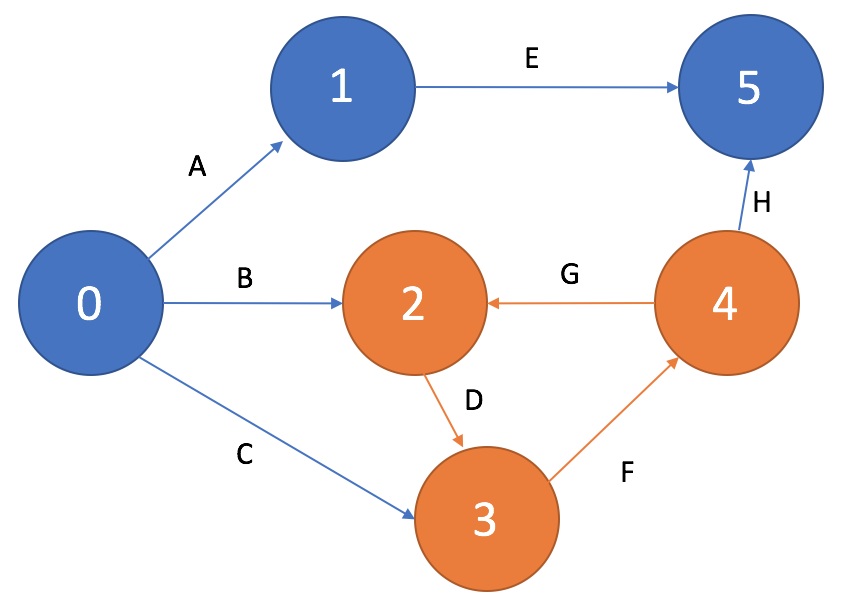
В таком случае необходимо проанализировать исходные данные и в зависимости от сделанных по итогам анализа выводов, либо перенаправить работу создающую цикл в другое событие (если работам, начинающимся в этом событии требуется ее результат, или если она является частью общего результата), либо совсем исключить ее из комплекса (если выявлено, что ее результат не требуется).
На рисунке 11 приведен пример устранения цикла, когда работа G становится частью общего результата.
Именование работ и нумерация событий
Каждая работа в сетевом графике должна определяться однозначно, только ей присущей парой событий, как и не должно быть на графике событий с одинаковыми номерами.
Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 0. Из исходного события вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 1. Затем вычеркивают работы, выходящие из события 1, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 2, и так продолжается до завершающего события.